Optimizing Fantasy Premier League Squad Selection Using Linear Programming for the 2024-2025 Season

Linear Programming is a mathematical technique aimed at maximizing or minimizing an objective function while adhering to certain constraints. As implied by its name, this method is applicable when both the objective function and the constraints are expressed as linear equations and inequalities.

Learn more about linearity here.

In this article, we will explore an intriguing application of Linear Programming: selecting the optimal Fantasy Premier League squad for the 2024-2025 season based on players' points from the previous season.

What is Fantasy Premier League?

Fantasy Premier League (FPL) is the official free-to-play fantasy football game of the English Premier League. Millions of participants set up their squads of players each season, competing to accumulate the most points. Points are awarded based on players' performances in real-life matches, including scoring goals, providing assists, or saving penalties.

Participants have a limited budget to spend on players, each of whom has a price. A squad consists of 15 players (2 goalkeepers, 5 defenders, 5 midfielders, and 3 forwards). Additionally, you can select a maximum of 3 players from any single Premier League team.

Check out the official Fantasy Premier League website.

Dataset

To create the best squad, we will use data on players' performances from the last season, aiming to maximize the total points scored by our selected team. We will utilize this dataset from Kaggle, which includes information on all Premier League players, their positions, teams, costs, and points scored in the previous season.

The following Python code extracts data from the CSV file and converts it into an array:

import pandas as pd
players_data_path = 'players.csv'
players_data = pd.read_csv(players_data_path)
features = ['name', 'now_cost', 'position', 'team', 'total_points']
X = players_data[features].dropna().sort_values(by='total_points', ascending=False)
player_np_array = X.to_numpy()

Player Object

To facilitate data manipulation, we define a Player class and convert our data into an array of Player objects:

# Define Player Object
class Player:
    def __init__(self, name, now_cost, position, team, total_points):
        self.name = name
        self.now_cost = now_cost
        self.position = position
        self.team = team
        self.total_points = total_points

# Convert to Player objects
players_array = [Player(player[0], player[1], player[2], player[3], player[4]) for player in player_np_array]

Linear Programming Model

We introduce a binary decision variable \( x_p \) for each player \( p \), where \( x_p = 1 \) if the player is selected and \( x_p = 0 \) otherwise. Our objective is to maximize the total points scored by the selected players:

Objective Function: Maximize \( \sum_{p} (x_p \cdot \text{points}_p) \) where \( p \) represents each player.

We impose the following constraints:

Budget Constraint: The total cost of selected players must not exceed the budget.
Team Constraint: No more than 3 players can be selected from the same Premier League team.
Position Constraints: The squad must include 2 goalkeepers, 5 defenders, 5 midfielders, and 3 forwards.

We use the mip library in Python to define and solve this model:

from mip import Model, xsum, maximize, BINARY

# Define model
model = Model(name="FPL", solver_name="CBC")
x = [model.add_var(name=f"x({player.name})", lb=0, ub=1, var_type=BINARY) for player in players_array]

# Objective function (maximize total points)
model.objective = maximize(xsum(x[i] * players_array[i].total_points for i in range(len(players_array))))

# Budget constraint
BUDGET = 1000
model.add_constr(xsum(x[i] * players_array[i].now_cost for i in range(len(players_array))) <= BUDGET)

# Team constraint
teams = {player.team for player in players_array}
max_team_players = 3
for t in teams:
    model.add_constr(xsum(x[i] * (players_array[i].team == t) for i in range(len(players_array))) <= max_team_players)

# Position constraints
position_limits = {'GKP': 2, 'DEF': 5, 'MID': 5, 'FWD': 3}
for pos, limit in position_limits.items():
    model.add_constr(xsum(x[i] * (players_array[i].position == pos) for i in range(len(players_array))) <= limit)

# Solve the problem
status = model.optimize(max_seconds=120)

Optimale Squad

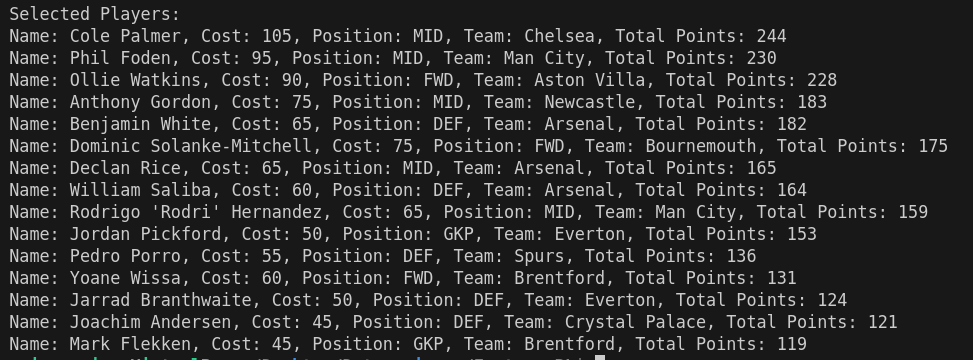
After adding few lines to display the selected squad and executing the python code, this is the Optimal Fantasy Premier League Squad:

Conclusion

While this method selects a Fantasy Premier League squad based on last season's performance, it's important to note that past performance may not always predict future outcomes. Nonetheless, it offers a valuable approach for initial squad selection.

This example demonstrates how Linear Programming can be employed to optimize a linear objective function subject to linear constraints. The mip library in Python provides a straightforward way to define and solve such optimization problems. Alternative Python libraries for solving Linear Programming problems include SciPy and PuLP.