EN FR

System of Equations

In various engineering and economics applications, we need to solve systems of equations.

A system of equations is a collection of equations sharing the same variables. It can be written as: 

f1(x1, x2, ..., xn) = a1
f2(x1, x2, ..., xn) = a2
...
fm(x1, x2, ..., xn) = am

Solving this system involves finding the variables x1, ..., xn that satisfy all equations.

System's size

The size of a system of equations is a crucial parameter when looking to solve it. We differentiate between two types of systems:

Fixed-Size Systems

Fixed-size systems are systems of equations where the number of equations and variables is known and remains constant. The number of variables and equations in these systems does not change when we change the problem’s input data.

Variable-Size Systems

Variable-size systems (also known as dynamic systems or adaptive systems) are systems where the number of equations and/or variables can change. For example, if we are modeling traffic flow in a city and forming an equation for each intersection, the number of equations in our system will vary depending on the city size. These types of systems require more vigilance because the growth of the system can be computationally expensive.

For fixed-size systems, we opt for simple methods unless the size of the matrix is huge. However, choosing an efficient method for variable-size systems is crucial because the system can grow and therefore increase the complexity of the solution.

Linearity of the System

Before exploring methods for solving systems of equations, it is fundamental to study the linearity of the system:

  • Linear Systems: Systems where each equation is linear.
  • Nonlinear Systems: Systems with at least one equation that is not linear.
Wonder what is a linear equation? Read here

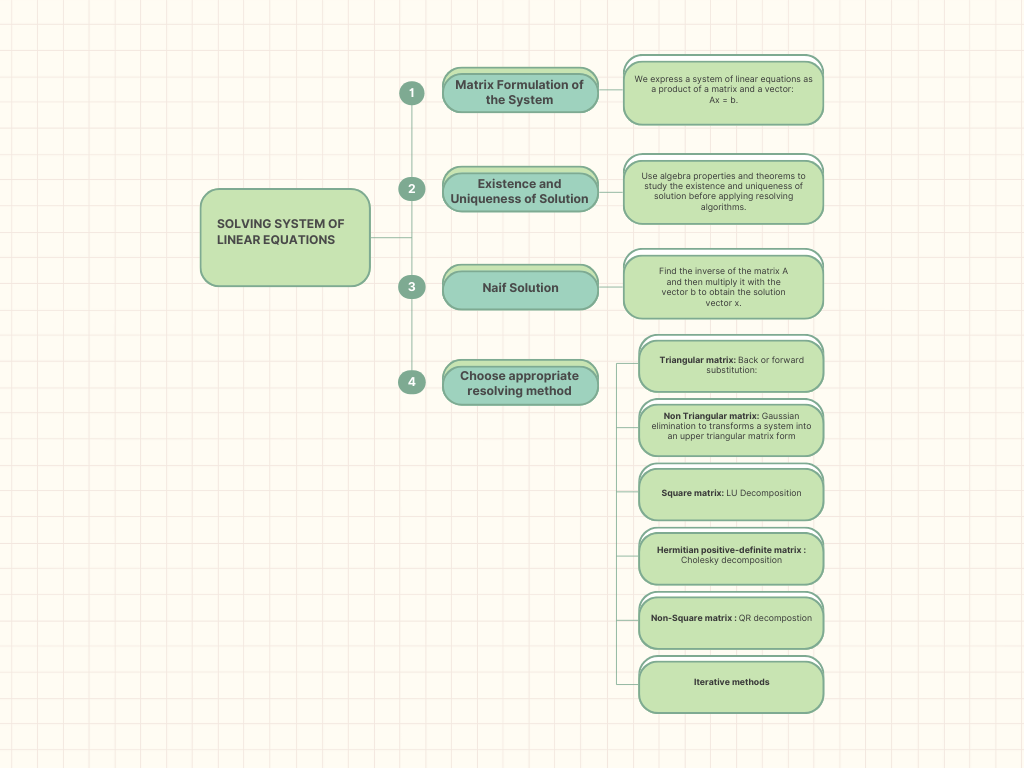
Existence and Uniqueness of Solutions

Once the type of the system is determined, we can study the existence and uniqueness of a solution:

  • No Solution: The system is inconsistent
  • Unique Solution: The system is consistent and independent.
  • Infinite Solutions: The system is consistent and dependent

Methods for Solving Systems of Equations

For solving systems of equations, different methods are used based on the type of system:

Nonlinear Systems

We offer one approach to solve nonlinear systems, which is Newton-Raphson method, though other methods exist.

Want to know how to solve a nonlinear system? Read here

Linear Systems

Linear systems are viewed as the following equation: \(\mathbf{A} \mathbf{x} = \mathbf{b}\)

We use matrix \(\mathbf{A}\) characteristics to choose the optimal method for solving the system, such as:

  • Matrix Inversion
  • Gaussian Elimination
  • LU Decomposition
This figure summarizes the approach to solve systems of linear equations. Summary for solving systems of linear equations
Want to explore details? Read here
Computing the solution of a system of linear equations or the decomposition of a matrix can be effectively be done using SciPy library, more specifically SciPy Linalg.