Optimisation de la sélection de l'équipe de Fantasy Premier League à l'aide de la Programmation Linéaire pour la saison 2024-2025

La Programmation Linéaire est une technique mathématique visant à maximiser ou minimiser une fonction objectif tout en respectant certaines contraintes. Comme son nom l'indique, cette méthode est applicable lorsque la fonction objectif et les contraintes sont exprimées sous forme d'équations et d'inégalités linéaires.

Dans cet article, nous explorerons une application intéressante de la Programmation Linéaire : sélectionner l'équipe optimale de Fantasy Premier League pour la saison 2024-2025 en se basant sur les points des joueurs de la saison précédente.

Qu'est-ce que Fantasy Premier League ?

Fantasy Premier League (FPL) est le jeu officiel de football fantasy gratuit de la Premier League anglaise. Des millions de participants configurent leurs équipes de joueurs chaque saison, en compétition pour accumuler le plus de points. Les points sont attribués en fonction des performances des joueurs dans les matchs réels, notamment en marquant des buts, en réalisant des passes décisives ou en arrêtant des penalties.

Les participants disposent d'un budget limité pour acheter des joueurs, chacun ayant un prix. Une équipe est composée de 15 joueurs (2 gardiens de but, 5 défenseurs, 5 milieux de terrain et 3 attaquants). De plus, vous pouvez sélectionner un maximum de 3 joueurs de la même équipe de Premier League.

Jeu de données

Pour créer la meilleure équipe, nous utiliserons les données sur les performances des joueurs de la saison dernière, en visant à maximiser le total des points marqués par notre équipe sélectionnée. Nous utiliserons ce jeu de données de Kaggle, qui inclut des informations sur tous les joueurs de la Premier League, leurs positions, équipes, coûts et points marqués la saison précédente.

Le code Python suivant extrait les données du fichier CSV et les convertit en un tableau :

import pandas as pd
players_data_path = 'players.csv'
players_data = pd.read_csv(players_data_path)
features = ['name', 'now_cost', 'position', 'team', 'total_points']
X = players_data[features].dropna().sort_values(by='total_points', ascending=False)
player_np_array = X.to_numpy()

Objet Joueur

Pour faciliter la manipulation des données, nous définissons une classe Joueur et convertissons nos données en un tableau d'objets Joueur :

# Définir l'objet Joueur
class Joueur:
    def __init__(self, name, now_cost, position, team, total_points):
        self.name = name
        self.now_cost = now_cost
        self.position = position
        self.team = team
        self.total_points = total_points

# Conversion en objets Joueur
players_array = [Joueur(player[0], player[1], player[2], player[3], player[4]) for player in player_np_array]

Modèle de Programmation Linéaire

Nous introduisons une variable binaire de décision \( x_p \) pour chaque joueur \( p \), où \( x_p = 1 \) si le joueur est sélectionné et \( x_p = 0 \) sinon. Notre objectif est de maximiser le total des points marqués par les joueurs sélectionnés :

Fonction Objectif : Maximiser \( \sum_{p} (x_p \cdot \text{points}_p) \) où \( p \) représente chaque joueur.

Nous imposons les contraintes suivantes :

• Contrainte de budget : Le coût total des joueurs sélectionnés ne doit pas dépasser le budget.
• Contrainte d'équipe : Pas plus de 3 joueurs ne peuvent être sélectionnés de la même équipe de Premier League.
• Contraintes de position : L'équipe doit comprendre 2 gardiens de but, 5 défenseurs, 5 milieux de terrain et 3 attaquants.

Nous utilisons la bibliothèque mip en Python pour définir et résoudre ce modèle :

from mip import Model, xsum, maximize, BINARY

# Définir le modèle
model = Model(name="FPL", solver_name="CBC")
x = [model.add_var(name=f"x({player.name})", lb=0, ub=1, var_type=BINARY) for player in players_array]

# Fonction objectif (maximiser les points totaux)
model.objective = maximize(xsum(x[i] * players_array[i].total_points for i in range(len(players_array))))

# Contrainte de budget
BUDGET = 1000
model.add_constr(xsum(x[i] * players_array[i].now_cost for i in range(len(players_array))) <= BUDGET)

# Contrainte d'équipe
teams = {player.team for player in players_array}
max_team_players = 3
for t in teams:
    model.add_constr(xsum(x[i] * (players_array[i].team == t) for i in range(len(players_array))) <= max_team_players)

# Contraintes de position
position_limits = {'GKP': 2, 'DEF': 5, 'MID': 5, 'FWD': 3}
for pos, limit in position_limits.items():
    model.add_constr(xsum(x[i] * (players_array[i].position == pos) for i in range(len(players_array))) <= limit)

# Résoudre le problème
status = model.optimize(max_seconds=120)

Équipe Optimale

Après avoir ajouté quelques lignes pour afficher l'équipe sélectionnée et exécuté le code python, voici la Meilleure équipe de Fantasy Premier League:

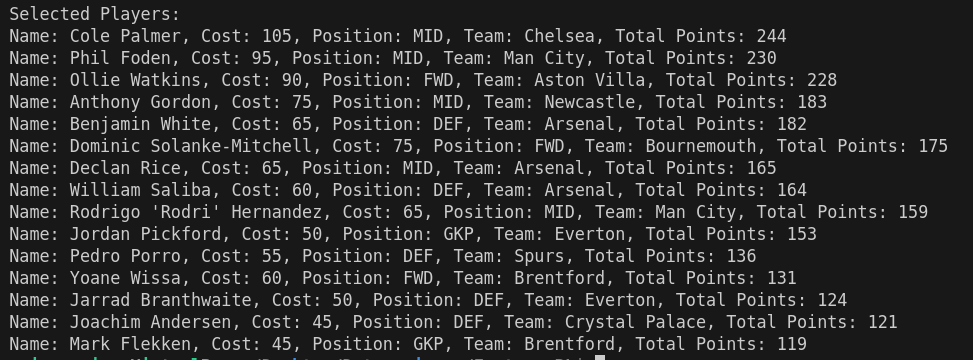
Conclusion

Bien que cette méthode permette de sélectionner une équipe de Fantasy Premier League basée sur les performances de la saison dernière, il est important de noter que les performances passées ne prédisent pas toujours les résultats futurs. Néanmoins, cela offre une approche précieuse pour la sélection initiale de l'équipe.

Cet exemple démontre comment la Programmation Linéaire peut être utilisée pour optimiser une fonction objectif linéaire sous contraintes linéaires. La bibliothèque mip en Python offre un moyen simple de définir et résoudre de tels problèmes d'optimisation. D'autres bibliothèques Python pour résoudre des problèmes de Programmation Linéaire incluent SciPy et PuLP.