Système d'Équations

Dans diverses applications en ingénierie et économie, nous devons résoudre des systèmes d'équations.

Un système d'équations est un ensemble d'équations partageant les mêmes variables. Il peut être écrit comme :

f1(x1, x2, ..., xn) = a1
f2(x1, x2, ..., xn) = a2
...
fm(x1, x2, ..., xn) = am

Résoudre ce système implique de trouver les variables x₁, ..., x_n qui satisfont toutes les équations.

Taille du système

La taille d'un système d'équations est un paramètre crucial lorsqu'on cherche à le résoudre. Nous différencions deux types de systèmes :

Systèmes de taille fixe

Les systèmes de taille fixe sont des systèmes d'équations où le nombre d'équations et de variables est connu et reste constant. Le nombre de variables et d'équations dans ces systèmes ne change pas lorsque nous changeons les données d'entrée du problème.

Systèmes de taille variable

Les systèmes de taille variable (également connus sous le nom de systèmes dynamiques ou systèmes adaptatifs) sont des systèmes où le nombre d'équations et/ou de variables peut changer. Par exemple, si nous modélisons le flux de trafic dans une ville et formons une équation pour chaque intersection, le nombre d'équations dans notre système variera en fonction de la taille de la ville. Ces types de systèmes nécessitent plus de vigilance car la croissance du système peut être coûteuse en calcul.

Linéarité du système

Avant d'explorer les méthodes de résolution des systèmes d'équations, il est fondamental d'étudier la linéarité du système :

• Systèmes linéaires : Systèmes où chaque équation est linéaire.
• Systèmes non linéaires : Systèmes avec au moins une équation qui n'est pas linéaire.

Existence et unicité des solutions

Une fois le type du système déterminé, nous pouvons étudier l'existence et l'unicité d'une solution :

• Pas de solution : Le système est incohérent
• Solution unique : Le système est cohérent et indépendant.
• Solutions infinies : Le système est cohérent et dépendant

Méthodes de résolution des systèmes d'équations

Pour résoudre les systèmes d'équations, différentes méthodes sont utilisées en fonction du type de système :

Systèmes non linéaires

Nous proposons une approche pour résoudre les systèmes non linéaires, qui est la méthode Newton-Raphson, bien que d'autres méthodes existent.

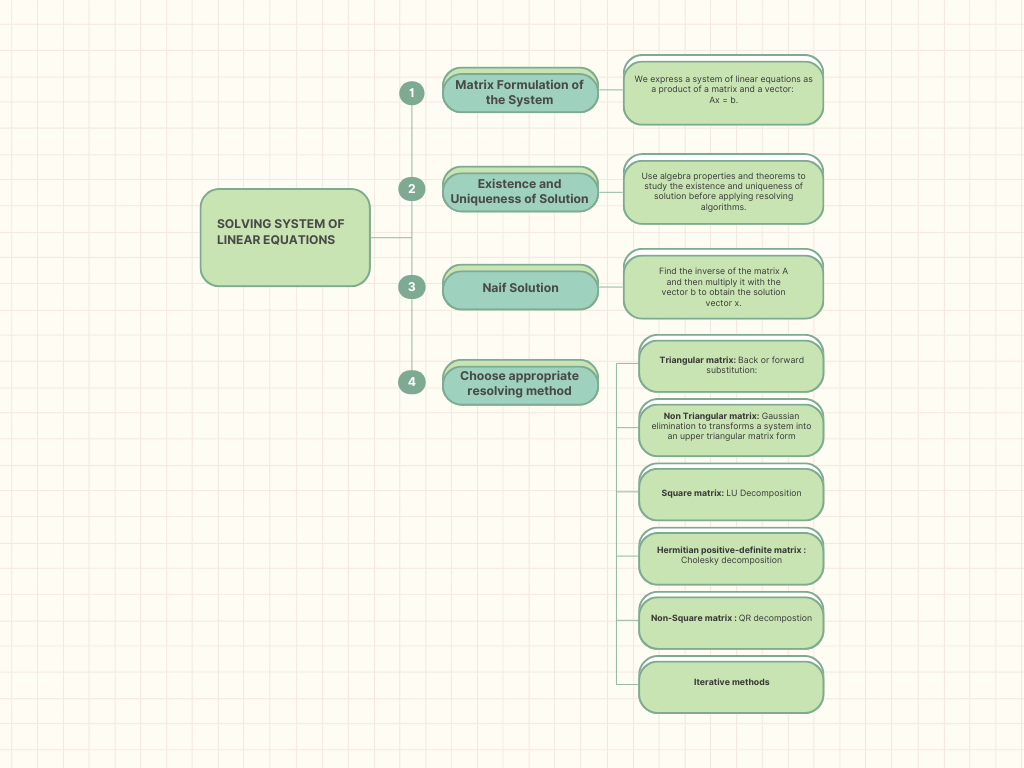
Systèmes linéaires

Un système linéaire peut s'écrire sous forme matricielle \(\mathbf{A} \mathbf{x} = \mathbf{b}\)

Nous utilisons les caractéristiques de la matrice \(\mathbf{A}\) pour choisir la méthode optimale de résolution du système, telles que :

• Inversion de matrice
• Élimination de Gauss
• Décomposition LU

Cette figure résume l'approche pour résoudre les systèmes d'équations linéaires.